# 数据结构
前端一般需掌握:数组、栈、队列、链表、树(二叉树)
# 数组
数组创建方法
// 第一种,也是最经常用的一种
const arr = [1, 2]
// 第二种,当我们不知道内部元素时
const arr = new Array(3) // [empty, empty, empty]
// 由第二种创建数组
const arr = (new Array(3)).fill(1)) // [1, 1, 1]
// 但是由fill创建的二维数组就会有局限性,因为fill一个引用类型的值的话,就会发生改变一个从而改变所有的情况
const arr = (new Array(3)).fill([])
arr[0].push(1)
console.log(arr) // [[1], [1], [1]]
一维数组和二维数组的区别
一维数组可以理解成一条直线 [1] 二维数组可以理解成一条平面,也就是数组中的元素为数组。比如 [[1], [1]]
二维数组的创建
const len = arr.length
const arr = []
for(let i = 0; i < len; i++) {
arr[i] = []
}
二维数组的访问
通过两层for循环访问二维数组
for (let i = 0; i < arr1.length; i++) {
for (let j = 0; j < arr1[i].length; j++) {
console.log(arr1[i][j])
}
}
一维数组用 for 循环遍历只需一层循环,二维数组是两层,三维数组就是三层。依次类推,N 维数组需要 N 层循环来完成遍历。
# 栈和队列
在JavaScript中,栈和队列的实现一般都是依赖于数组,大家完全可以把栈和队列看成特别的数组
(注:实际上,栈和队列作为两种运算受限的线性表,用链表来实现也是没问题的。只是从前端面试做题的角度来说,基于链表来实现栈和队列约等于脱裤子放屁(链表实现起来会比数组麻烦得多,做不到开箱即用),基本没人会这么干。这里大家按照数组的思路往下走就行了)
两者的区别在于,它们各自对数组的增删操作有着不一样的限制
数组的增
const arr = [1,2]
arr.unshift(0) // [0,1,2] 添加到元素头部
arr.push(3) // [0, 1, 2, 3]添加到数组尾部
arr.splie(1, 0 , 4) // [0, 4, 1, 2, 3] // 改变任意位置元素,增或者删或者替换
数组的删
const arr = [1, 2, 3, 4]
arr.shift() // [2, 3, 4] 删除头部元素
arr.pop() // [2, 3] 删除尾部元素
arr.splie(0, 1) // [3] 删除从下标0开始的一个元素
# 栈
栈是一种后进先出的数据结构,在js中其实是只能用pop和push完成增删的"数组"
两个特征
- 只允许从尾部添加元素
- 只允许从尾部取出元素
对应到数组中,就是push和pop方法。因此,在JavaScript中,栈就是限制只能用push添加元素,用pop来删除元素的一种特殊数组
const stack = []
stack.push(1)
stack.push(2)
stack.push(3)
// 入栈
while(stack.length) {
const now = stack[stack.length - 1]
console.log('当前出栈元素', now)
stack.pop()
}
console.log(stack) // []
# 队列
队列是一种先进先出的数据结构,在js中其实就是只用push和shift完成增删的"数组"
特征
- 只允许从尾部添加元素
- 只允许从头部移除元素
const queue = []
// 入队
queue.push(1)
queue.push(2)
queue.push(3)
// 出队
while(queue.length) {
const now = queue[0]
console.log('出队元素', now)
queue.shift()
}
console.log(queue) // []
总结:在栈元素出栈时,我们关心的是栈顶元素(数组的最后一个元素)。队列元素出队时,我们关心的是队头元素(数组的第一个元素)
# 链表
链表和数组相似,它们都是有序的列表、都是线性结构(有且仅有一个前驱,有且仅有一个后继)。
不同点在于,链表中,数据单位的名称叫做结点,而结点和结点的分布,在内存中可以是离散的。
这个“离散”是相对于数组的“连续”来说的。
JS 中的链表,是以嵌套的对象的形式来实现的,每一个结点的结构都包括了两部分的内容:数据域和指针域:
{
// 数据域
val: 1,
// 指针域,指向下一个结点
next: {
val:2,
next: ...
}
}
需要值得注意的是结点的插入以及删除
插入
在node1和node2中插入node3,其实就是将node1的next指向node3
// 如果目标结点本来不存在,那么记得手动创建
const node3 = new ListNode(3)
// 把node3的 next 指针指向 node2(即 node1.next)
node3.next = node1.next
// 把node1的 next 指针指向 node3
node1.next = node3
删除
在node1和node2之间删除node3,node3会被垃圾回收机制回收
node1.next = node3.next
链表的增删逻辑空间复杂度为 O(1)
数组的增删逻辑空间复杂度为 O(n) 线性增长
但是通过arr[1]的形式去访问元素,空间复杂度会降为常数级别 O(1)
# 树
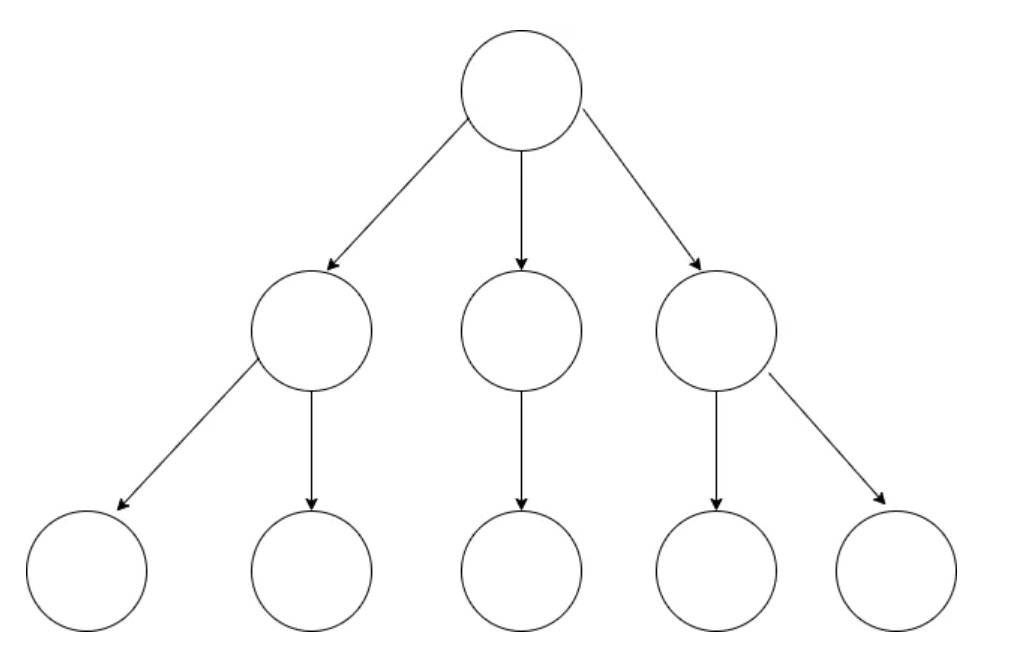
树的概念与特性
- 树的层次计算规则:根节点所在的那一层为第一层,其子节点为第二层,以此类推
- 结点和树的“高度”计算规则:叶子结点高度记为1,每向上一层高度就加1,逐层向上累加至目标结点时,所得到的的值就是目标结点的高度。树中结点的最大高度,称为
“树的高度” “度”的概念:一个结点开叉出去多少个子树,被记为结点的“度”,比如图中,根节点的“度”就是3叶子结点:叶子结点就是度为0的结点。在上图中,最后一层的结点全为0,所以这一层的结点称为叶子结点
# 二叉树
二叉树指满足以下要求的树:
- 它可以没有根节点,作为一颗空树存在
- 左右两边结点不可互换
- 如果它不是空树,那么必须由根节点、左子树和右子树组成,且左右子树都是二叉树。左右树同样遵循可以为空。如下图
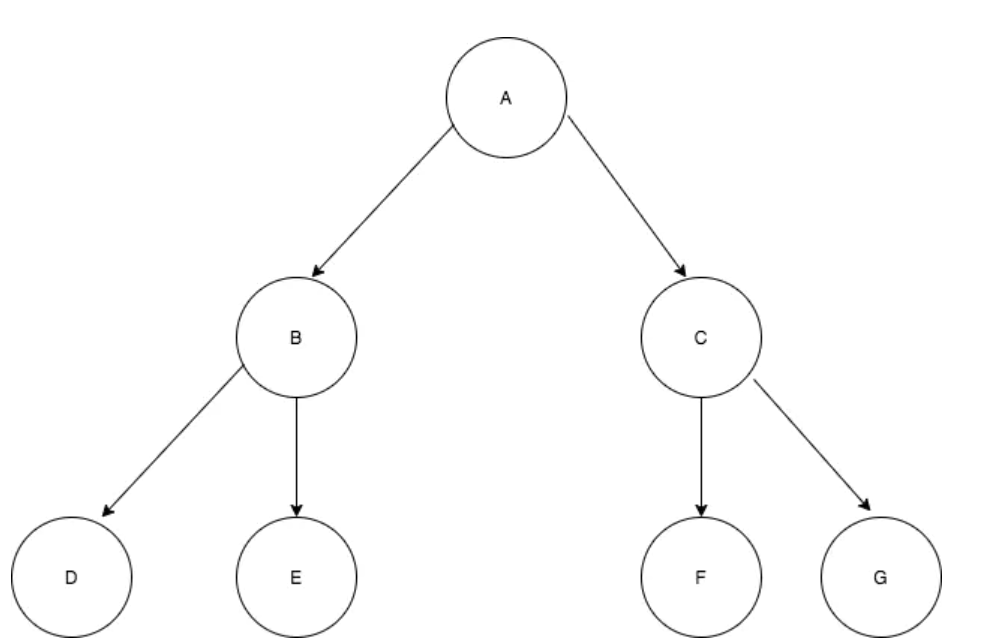
二叉树中的结点结构:
- 数据域
- 左树指针
- 右树指针
用js定义二叉树
// 二叉树结点的构造函数
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
// 当你需要新建一个二叉树结点时,直接调用构造函数、传入数据域的值就行了:
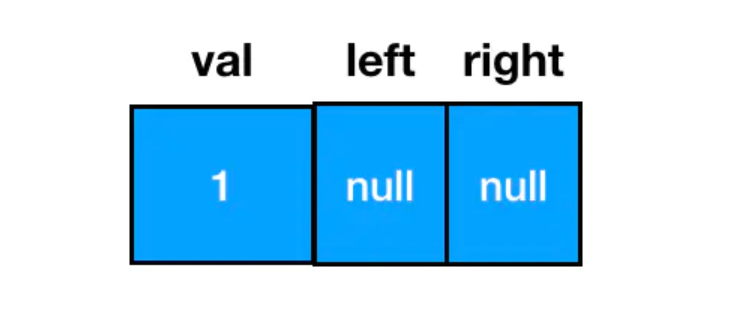
const node = new TreeNode(1)
如此便能得到一个值为 1 的二叉树结点,从结构上来说,它长这样
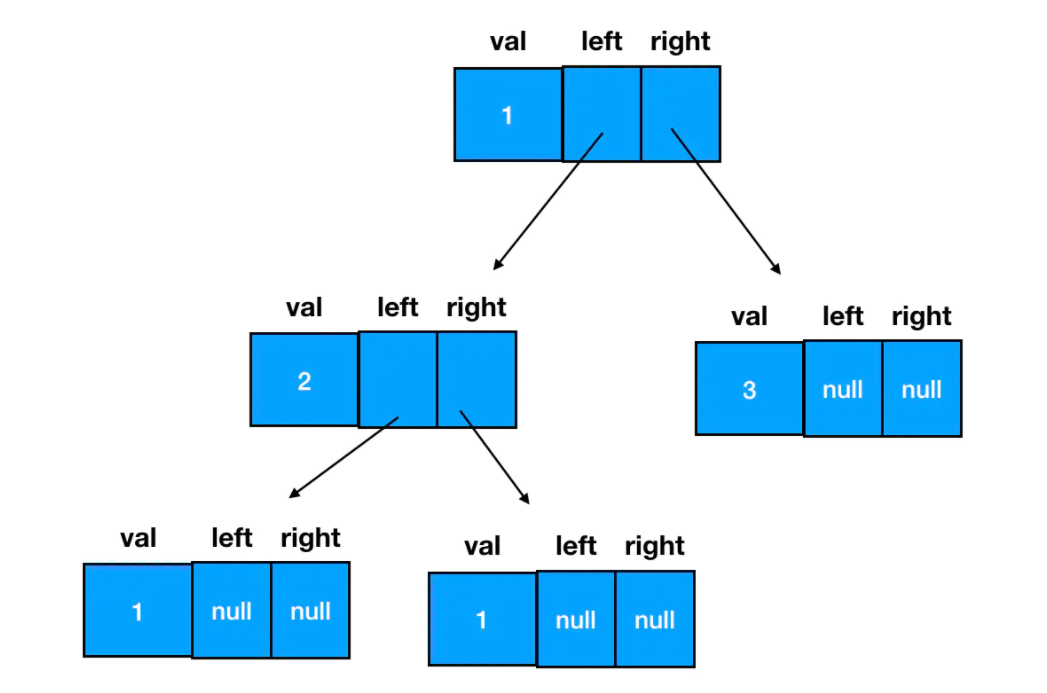
可以料想到一颗完整的二叉树长这样
最大深度 →